本文最后更新于：1 个月前

[TOC]

关于字符串转换整数 (atoi) 的思考

前言

最近解了一道 LeetCode 中的算法题: 8.字符串转换整数 (atoi) ，描述如下:

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

1. 读入字符串并丢弃无用的前导空格
2. 检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。 确定最终结果是负数还是正数。 如果两者都不存在，则假定结果为正。
3. 读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
4. 将前面步骤读入的这些数字转换为整数（即，"123" -> 123， "0032" -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤 2 开始）。
5. 如果整数数超过 32 位有符号整数范围 [−2^31,  2^31 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −2^31 的整数应该被固定为 −2^31 ，大于 2^31 − 1 的整数应该被固定为 2^31 − 1 。
6. 返回整数作为最终结果。

在 AC 后，看了官方和其他人的题解，了解到了一个不曾涉及到过的知识点:有限状态机 (Finite State Automaton) 和确定性有限自动机 (Deterministic Finite Automaton, DFA)。

因此在这里记录一下解决这个题目，并学习这个新知识点的过程。

解法一、正则表达式 “^ *([\\-\\+]?[0-9]+)”

提取有效整数字符串

在最开始看到这个题目的时候，厘清题干对数字有效性的要求后，可以将这个特征提取为以下正则表达式:

^ *([\\-\\+]?[0-9]+)

根据题干的第一点，我们可知，字符串可能存在前导空格，因此我们这里用 ^ * 来匹配字符串起始位置的 0 个或多个 ‘ ‘ 空格。

然后题干第 2 点表明，可能存在正负符号，用于解释当前待转换字符串整数的正负性。这里需要注意，**’+/-‘ 符号只能为 0 个或 1 个**。因为根据第 3 点的描述，在读入正负号后，下一个字符如果为非数字字符，则剩余部分会被全部忽略。所以我们使用 [\\-\\+]? 来匹配 0 个或 1 个 ‘-‘ 或 ‘+’ 符号。

在去掉前导空格和读取正负符号后，只能是数字字符，并且应该是** 1 个或多个**时，当前数字才有效。所以用 [0-9]+ 来匹配 1 个或多个数字字符。

通过这个正则表达式即可判断当前字符串是否能被转换为有效的整数，并且使用 () 的子表达式方法可以直接提取出整数的有效部分。

// 使用正则表达式和 std::stoi 
class Solution {
public:
    int myAtoi(std::string s) {
        std::regex re("^ *([\\+\\-]?[0-9]+)");
        std::smatch m;
        std::string sub;
        if (regex_search(s, m, re)) {
            if (m.size() > 1) {
                sub = m[1].str();
            }
        }
        if (sub.size() == 0) {
            return 0;
        } else {
            try {
                return std::stoi(sub.c_str());
            } catch (std::exception& e) {
                return sub[0] == '-' ? INT_MIN : INT_MAX;
            }
        }
        return 0;
    }
};

当然要转换成数字还有一个 signed int 类型的溢出问题。

signed int 溢出判断

溢出判断时每个解法都需要考虑的问题，后续几种解法中的溢出判断也都是这一章节中所提到的，因此在后续解法中不在重复描述。

std::stoi 和 out of range

最开始的时候，为了方便，直接使用 std::stoi 来进行转换，这个函数能直接转换带 ‘+’ 和 ‘-‘ 的整数，并且在溢出时会抛出 “out of range” 的异常，因此只要一个 try-catch 就可以解决，具体应用可见上一节中给出的代码示例。

字符串比较

如果说使用 std::stoi 也太犯规了，那么换种思路，通过整数字符串 s 和 INT_MIN (-2147483648), INT_MAX (2147483647) 的字符串进行比较，也是一种判断溢出的方法。并且该方法在判断完成后再转换为 int 类型，一定不会造成溢出问题。

使用字符串比较需要注意两个点:

整数字符串可能存在 ‘+/-‘ 符号，比较前需要统一，即两个字符串要么都有符号，要么都没有符号；
比较过程中需保持整数字符串 s 和 INT_MIN, INT_MAX 字符串长度一致，较短字符串前部追加 ‘0’ 字符；

乘法判断

由于 string 转换成 int 是必经之路，因此我们在逐位转换过程中直接比较乘法结果是否溢出即可。

一个整数字符串 s 转换成整数 (不考虑符号，因为不考虑符号的情况下判断溢出，永远只需要判断 ‘>’ 即可，可有效减少判断条件数量) 的过程，只需要重复计算 num = num * 10 + s[i] - '0'，这里我们限制只能使用 int 类型存储 res，因此我们需要在每次计算之前就进行判断，否则在计算过程中会提示溢出错误。

if (溢出) {
  return (符号 == '-') ? INT_MIN : INT_MAX;
} else {
  num = num * 10 + s[i] - '0';
}

会溢出的情况有以下几种：

当前为负数，且 num > INT_MAX / 10 (为什么是 INT_MAX / 10？因为此时的 num 不考虑符号，那么 INT_MAX / 10 和 -INT_MIN / 10 结果是一样的，都等于 ‘214748364’)；
当前为负数，且 num == INT_MAX / 10 且 s[i] > ‘8’;
当前为正数，且 num > INT_MAX / 10;
当前为正数，且 num == INT_MAX / 10 且 s[i] > ‘7’;

看似有 4 种情况，但是实际上，我们可以将问题优化为 2 种情况：

num > INT_MAX / 10;
num == INT_MAX / 10 且 s[i] > ‘7’;

为什么正数和负数的情况下，一个是 s[i] > '7'，一个是 s[i] > '8' 可以统一为 s[i] > 7 呢？

这是因为当负数 num == INT_MAX / 10 且 s[i] == ‘8’ 时，我们假定此时已经溢出直接返回 INT_MIN ，和未溢出继续计算 num = num * 10 + s[i] - '0' 的结果都是 INT_MIN。

但是继续计算的话，由于我们在此前将 num 符号去除了，也就意味着 num 作为一个非负数始终应该小于 INT_MAX，但是当 num == INT_MAX / 10 且 s[i] == ‘8 时，结果已经溢出了。

所以我们不妨将这种情况也视为已溢出，将溢出条件极大的简化。

if (num > INT_MAX / 10 || (num == INT_MAX / 10 && s[i] > '7')) {
  return (符号 == '-') ? INT_MIN : INT_MAX;
} else {
  num = num * 10 + s[i] - '0';
}

解法二、确定性有限状态机 (DFA)

状态机

状态机（State Machine）是一种抽象的计算模型，用于描述一个系统或算法在不同状态之间的转换和行为。它可以被用来建模各种问题，从简单的逻辑控制到复杂的软件系统。状态机通常由以下几个部分组成：

状态（State）： 系统可能处于的不同状态。每个状态代表系统的某种特定行为或情况。例如，自动售货机可以处于”待命”、”投币”、”出售”等状态。
事件（Event）： 引起状态转换的外部或内部事件。当事件发生时，系统可以从当前状态转移到新的状态。例如，自动售货机可能会接收到”投币”、”选择商品”等事件。
转移（Transition）： 从一个状态到另一个状态的过渡，通常与事件相关联。转移描述了当某个特定事件发生时系统如何从一个状态切换到另一个状态。
动作（Action）： 在状态转换时执行的操作或行为。动作可以是更新内部状态、输出信息、执行计算等。例如，当自动售货机从”投币”状态转移到”出售”状态时，会扣除相应金额并输出商品。
初始状态（Initial State）： 系统在开始时所处的状态。
终止状态（Final State）： 系统的终止状态，表示系统已经完成了某个任务或达到了某个目标。

状态机可以分为有限状态机（Finite State Machine，FSM）和无限状态机（Infinite State Machine）。在有限状态机中，状态的数量是有限的，状态之间的转换也是有限的；而在无限状态机中，状态的数量是无限的，状态之间的转换也可以是无限的。

状态机在计算机科学领域有着广泛的应用，例如在编译器设计、网络协议分析、游戏开发等方面都能看到它的身影。

确定性有限状态机（Deterministic Finite Automaton，DFA）

确定性有限状态机（Deterministic Finite Automaton，DFA）是有限状态机（Finite State Machine，FSM）的一个子集。DFA 是一种特殊类型的有限状态机，其特点是在给定状态和输入字符的情况下，只有一种确定的状态转移路径。

与一般的有限状态机相比，确定性状态机具有以下不同之处：

确定性： DFA 在任何给定时刻都有一个唯一的状态，且从当前状态和输入字符出发只能转移到一个确定的下一个状态。这种确定性使得 DFA 在状态转移和行为方面更加可预测和简单。
状态转移表： DFA 可以使用状态转移表来描述状态之间的转移关系。在状态转移表中，每一行代表一个状态，每一列代表一个输入字符，表格中的每个元素表示从当前状态经过对应输入字符转移到的下一个状态。这种表格形式的表示使得 DFA 的状态转移过程变得直观和易于理解。
非确定性： 与非确定性有限状态机（Non-deterministic Finite Automaton，NFA）相比，DFA 不允许存在一个状态在给定输入字符的情况下具有多个可能的转移路径。这种特性使得 DFA 在状态转移和行为方面更加确定和可靠。

总的来说，确定性状态机是有限状态机中的一种特殊形式，它的确定性和简单性使得它在许多实际应用中得到了广泛的应用，例如在编译器设计、字符串匹配算法、网络协议分析等领域。

题解

这里直接引用 LeetCode 官方题解中的图示，方便理解。

状态定义

根据题干，我们可以定义这几个状态：

起始空格状态 (start)： 从起始位置开始的空格状态；
符号位状态 (signed)： 正负号位状态；
数字状态 (in_number)： 数字状态；
结束状态 (end)： 结束状态；

事件

在这个算法题中，事件即读取一个字符。

状态转移表

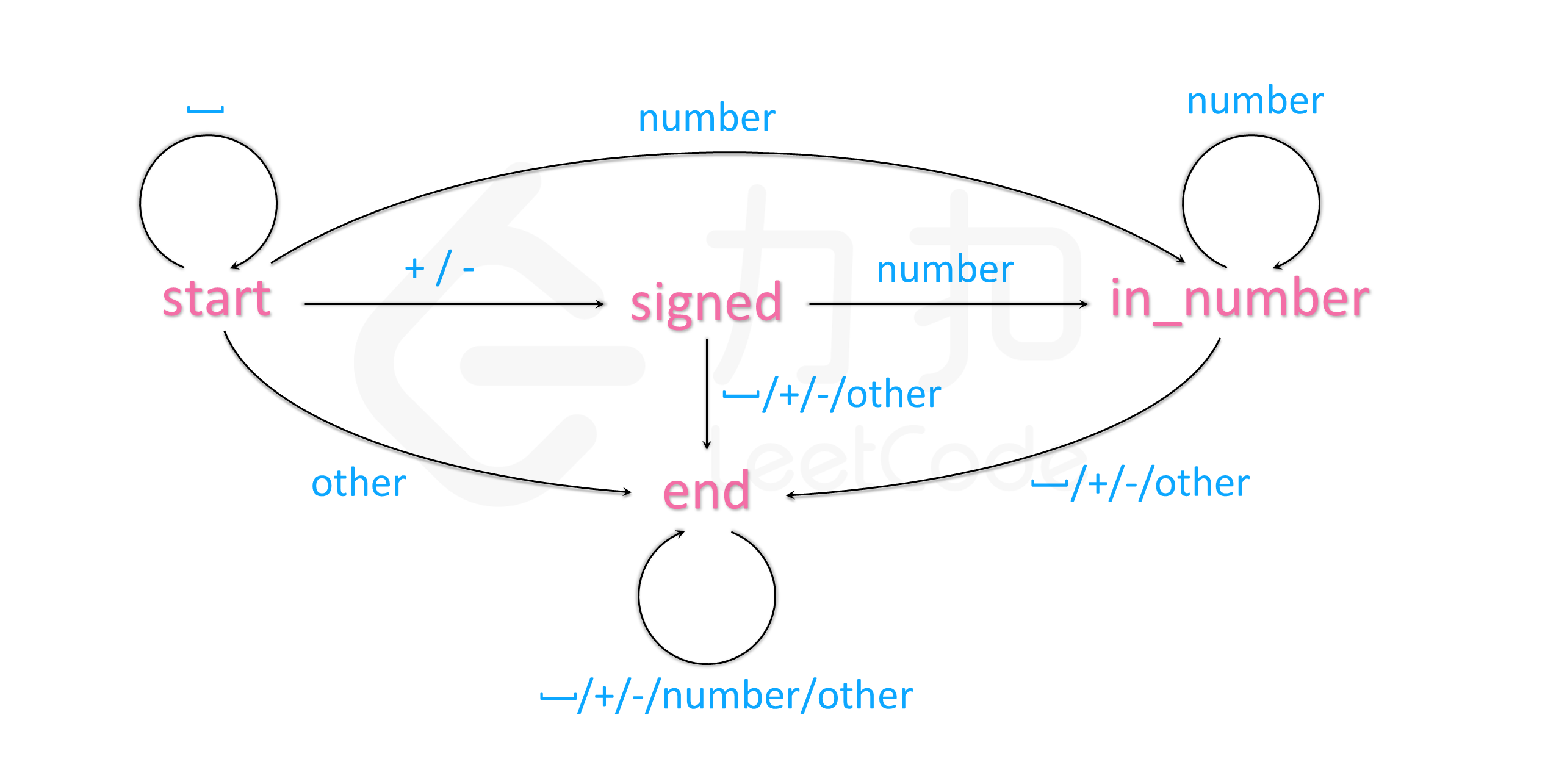
状态转移图

可以看出，每读取一个字符，对应的状态均是唯一确定的，因此根据上图，我们可以得到以下状态转移表：

state	‘ ‘	+/-	number	other
start	start	signed	in_number	end
signed	end	end	in_number	end
in_number	end	end	in_number	end
end	end	end	end	end

我们可以直接使用一个 std::unordered_map<std::string, std::vector<std::string>> 来表示这个状态转移表：

std::unordered_map<std::string, std::vector<std::string>> stat_tb = {
  {"start", {"start", "signed", "in_number", "end"}},
  {"signed", {"end", "end", "in_number", "end"}},
  {"in_number", {"end", "end", "in_number", "end"}},
  {"end", {"end", "end", "end", "end"}}
};

代码实现

有了上面的状态转移表，我们只需要每读取一个字符，然后判断状态，并转移状态，在转换整数时结合上一章节中提到的溢出判断，即可完成字符串到整数的转换。

// 利用 DFA (确定性有限自动机) 解决该问题
class Solution {
 private:
  // 设置状态转移表
  std::unordered_map<std::string, std::vector<std::string>> stat_tb = {
    {"start", {"start", "sign", "num", "end"}},
    {"sign", {"end", "end", "num", "end"}},
    {"num", {"end", "end", "num", "end"}},
    {"end", {"end", "end", "end", "end"}},
  };

  // 根据当前输入字符，获取状态
  int getch(char c) {
    if (c == ' ') return 0;
    if (c == '+' || c == '-') return 1;
    if (isdigit(c)) return 2;
    return 3;
  }

 public:
  int myAtoi(std::string s) {
    int num = 0, sign = 1, lim_a = INT_MAX / 10, lim_b = INT_MAX % 10;
    std::string stat = "start";
    
    for (char c : s) {
      // 此处使用下标的方式读取当前字符输入状态转移结果，极大简化了判断条件
      stat = stat_tb[stat][getch(c)];
      if (stat == "sign") {
        sign = c == '-' ? -1 : 1;
      }
      if (stat == "num") {
        // 溢出判断
        if (num > lim_a || (num == lim_a && c - '0' > lim_b)) {
          return sign == -1 ? INT_MIN : INT_MAX;
        }
        num = num * 10 + (c - '0');
      }
      if (stat == "end") break;
    }
    return num * sign;
  }
};

官方题解中使用 map 和 vector 的组合来存储状态转移表，并且通过下标的方式读取输入字符后状态转移的结果，这一设计非常巧妙，值得学习。

当然我们单纯使用 if-else 完成判断并转移状态，也是可以的，只不过代码会相对长一些，这也是我在了解状态机后手搓的代码：

class Solution {
private:
    enum State { Start, Signed, Number, End };

public:
    int myAtoi(std::string s) {
        int stat_ = Start, num_ = 0, sig_ = 1;
        int lim_a = INT_MAX / 10, lim_b = INT_MAX % 10;
        for (char ch : s) {
            switch (stat_) {
            case Start: {
                if (ch == ' ') {
                    stat_ = Start;
                } else if (ch == '+' || ch == '-') {
                    stat_ = Signed;
                    sig_ = (ch == '-') ? -1 : 1;
                } else if (isdigit(ch)) {
                    stat_ = Number;
                    num_ = num_ * 10 + (ch - '0');
                } else {
                    stat_ = End;
                }
                break;
            }
            case Signed: {
                if (isdigit(ch)) {
                    stat_ = Number;
                    num_ = num_ * 10 + (ch - '0');
                } else {
                    stat_ = End;
                }
                break;
            }
            case Number: {
                if (isdigit(ch)) {
                    if (num_ > lim_a || (num_ == lim_a && ch - '0' > lim_b)) {
                        return sig_ == -1 ? INT_MIN : INT_MAX;
                    } else {
                        num_ = num_ * 10 + (ch - '0');
                    }
                } else {
                    stat_ = End;
                }
                break;
            }
            case End: {
                return num_ * sig_;
            }
            }
        }
        return num_ * sig_;
    }
};

吐槽一句，使用 std::unordered_map<std::string, std::vector<std::string>> 的代码看起来简洁很多，但是在实际运行时，和使用 if-else 的代码相比，性能差距大的不是一点半点…使用上面第二种我手搓的代码，AC 显示耗时 0ms，但是官方题解需要 11 ms…所以也不能一味的追求代码的简短囧。。

总结

在工作业务中，如果并非追求极致的造轮子，合理应用正则表达式和标准库函数来解决业务问题，也不失为一种好的选择；
溢出边界的判断条件优化，是简化代码的关键；
使用确定性有限状态机解决这类问题（有输入，根据输入可确定唯一状态），是一种非常清晰好理解，并且简洁的解决方案；

程序员进阶

#原创 #leetcode #确定有限状态机 #DFA

关于字符串转换整数 (atoi) 的思考

https://ccccx159.github.io/2024/04/11/关于字符串转整数算法题的思考/

作者

Xu@n Ch3n

发布于

2024年4月11日

更新于

2024年4月12日

许可协议

12. 整数转罗马数字上一篇

Media-Download-Helper 项目说明下一篇