10. 正则表达式匹配

题目描述

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

• ‘.’ 匹配任意单个字符
• ‘*’ 匹配零个或多个前面的那一个元素
• 所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

• 1 <= s.length <= 20
• 1 <= p.length <= 20
• s 只包含从 a-z 的小写字母。
• p 只包含从 a-z 的小写字母，以及字符 . 和 *。
• 保证每次出现字符 * 时，前面都匹配到有效的字符

题解

解法一：动态规划

以下题解思路和图片，引用自：

作者：笨猪爆破组

链接：https://leetcode.cn/problems/regular-expression-matching/solutions/1/shou-hui-tu-jie-wo-tai-nan-liao-by-hyj8/

从左往右扫的话

• 字符后面是否跟着星号会影响结果，分析起来有点复杂。
  

选择从右往左扫描

• 星号的前面肯定有一个字符，星号也只影响这一个字符，它就像一个拷贝器。
  

• s、p 串是否匹配，取决于：最右端是否匹配、剩余的子串是否匹配。

• 只是最右端可能是特殊符号，需要分情况讨论而已。

通用地表示出子问题

• 大子串是否匹配，和剩余子串是否匹配，是规模不一样的同一问题。
  

情况1：s[i−1] 和 p[j−1] 是匹配的

• 最右端的字符是匹配的，那么，大问题的答案 = 剩余子串是否匹配。
  

情况2：s[i−1] 和 p[j−1] 是不匹配的

• 右端不匹配，还不能判死刑——可能是 p[j−1] 为星号造成的不匹配，星号不是真实字符，它不匹配不算数。
• 如果 p[j−1]p[j-1]p[j−1] 不是星号，那就真的不匹配了。
  

1. p[j−1]==”∗”，且 s[i−1] 和 p[j−2] 匹配
   • p[j−1] 是星号，并且 s[i−1] 和 p[j−2] 匹配，要考虑三种情况：
     • p[j−1] 星号可以让 p[j−2] 在 p 串中消失、出现 1 次、出现 >=2 次。
     • 只要其中一种使得剩余子串能匹配，那就能匹配，见下图 a1、a2、a3。
       
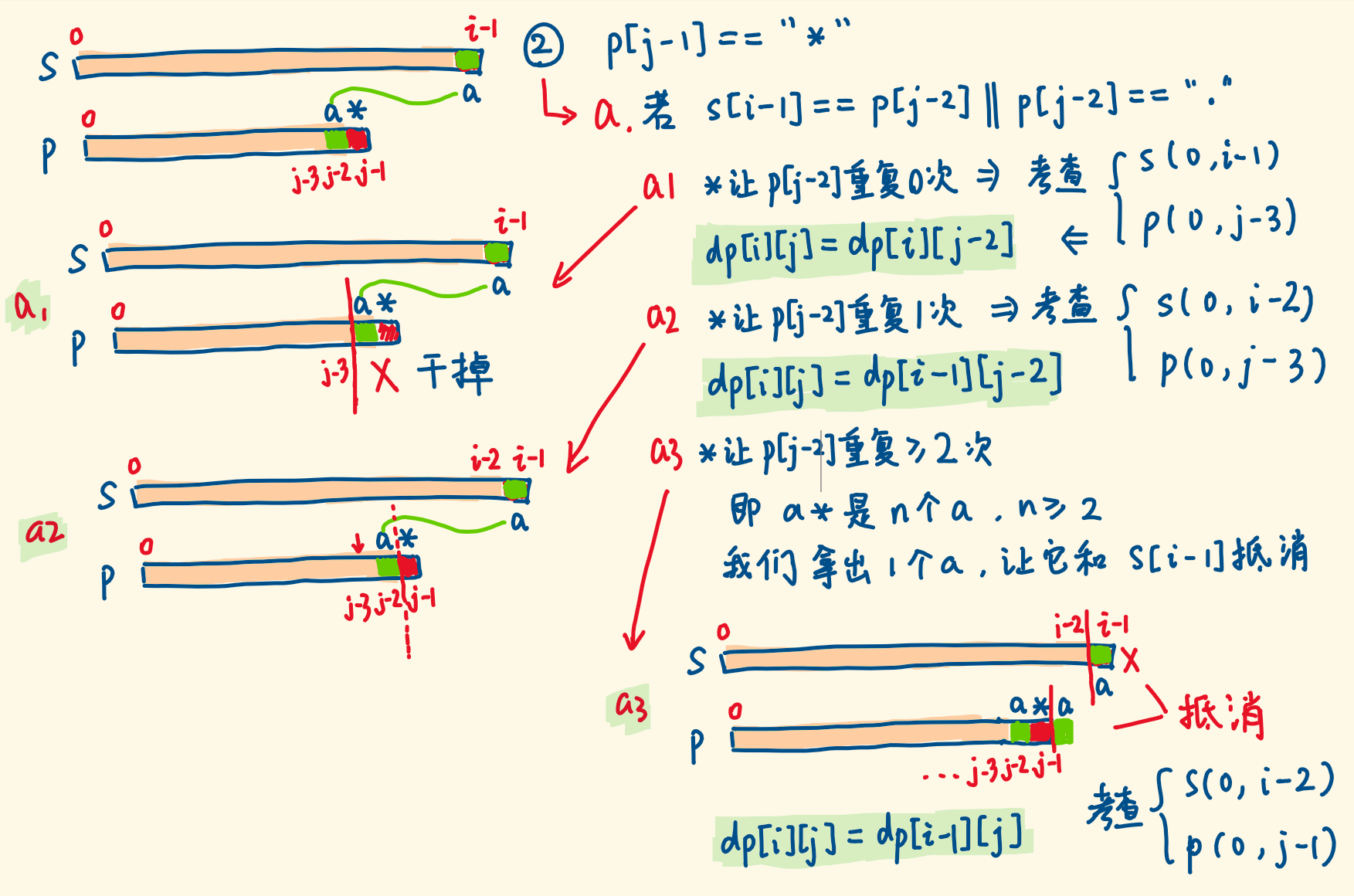
     • a3 情况：假设 s 的右端是一个 a，p 的右端是 a * ，* 让 a 重复 >= 2 次
       • 星号不是真实字符，s、p是否匹配，要看 s 去掉末尾的 a，p 去掉末尾一个 a，剩下的是否匹配。
       • 星号拷贝了 >=2 个 a，拿掉一个，剩下 >=1 个a，p 末端依旧是 a* 没变。
       • s 末尾的 a 被抵消了，继续考察 s(0,i-2) 和 p(0,i-1) 是否匹配。
2. p[j−1]==”∗”，但 s[i−1] 和 p[j−2] 不匹配
   • s[i−1] 和 p[j−2] 不匹配，还有救，p[j−1] 星号可以干掉 p[j−2]，继续考察 s(0,i−1) 和 p(0,j−3)。
     

base case

• p 为空串，s 不为空串，肯定不匹配。
• s 为空串，但 p 不为空串，要想匹配，只可能是右端是星号，它干掉一个字符后，把 p 变为空串。
• s、p 都为空串，肯定匹配。

代码实现

class Solution {
public:
  bool isMatch(std::string s, std::string p) {
    int s_len = s.size(), p_len = p.size(), i = 0, j = 0;
    if (s_len > 0 && p_len <= 0) return false;
    // 申请 dp
    std::vector<std::vector<bool>> dp(s_len + 1,
                                      std::vector<bool>(p_len + 1, false));

    // 边界
    // 1. s, p 均为空串
    dp[0][0] = true;
    // 2. s 为空串，p 不为空，则 p 必须以 * 结尾
    for (int j = 2; j <= p_len; j++) {
      if (p[j - 1] == '*') dp[0][j] = dp[0][j - 2];
    }
    // 3. s 不为空，p 为空，初始化时默认已经全部设为false了

    // 状态转移，i 和 j 表示的时长度，并非真实下标
    for (j = 1; j <= p_len; j++) {
      for (i = 1; i <= s_len; i++) {
        if (s[i-1] == p[j-1] || p[j-1] == '.') {      // 当 s[i-1] 和 p[j-1] 匹配，则状态转移为 dp[i-1][j-1]
          dp[i][j] = dp[i-1][j-1];
        } else if (p[j-1] == '*') {                   // 当 s[i-1] 和 p[j-1] 不匹配时，考虑 p[j-1] 为 * 号
          if (s[i-1] == p[j-2] || p[j-2] == '.') {
            // 当 s[i-1] 和 p[j-2] 匹配，则考虑 * 抵消 0 次，1 次和 多次
            // 0   次：i 不变，j-2
            // 1   次：i-1, j-2
            // >=2 次：i-1，j 不变
            dp[i][j] = dp[i-1][j-2] || dp[i-1][j] || dp[i][j-2];
          } else {
            // 当 s[i-1] 和 p[j-2] 不匹配时，由于 * 号可表示前置字符出现0次，因此 p 中去除这两个字符 j - 2 后继续匹配
            dp[i][j] = dp[i][j-2];
          }
        }
      }
    }
    return dp[s_len][p_len];
  }
};

总结

1. 逆序思考问题，从右往左扫描，可以简化问题；
2. 状态转移方程的推导，需要考虑多种情况，包括星号的作用；
3. 边界条件的处理，需要考虑 s、p 为空串的情况；